Der alte Spruch "Ob hoch oder runter, halte immer etwas drunter" hat seine Grundlage in dem Wissen, dass ein abgefeuertes Geschoss sich im Schwerkraftfeld der Erde bewegt. Hier mischt also die Physik kräftig mit. Inwiefern sie dies macht, erklären wir Euch mit diesem Artikel.
Was ist die gravimetrische Entfernung?
Kurzum, die Entfernung die ein Geschoss unter Einflussnahme der Anziehungskraft (Schwerkraft) zurück legt. Alles was fliegt möchte auch wieder runter, so auch unser Projektil nach dem Abfeuern und die Schwerkraft sorgt dafür, dass dies auch geschieht. Da die Erdanziehung die wichtigste Kraft ist, die auf Euer Geschoss einwirkt, gilt es diese also stets zu beachten.
Schießt man hierbei auf ein horizontales Ziel (Abschusspunkt-Höhe = Zielhöhe) mit z.B. 1000m Entfernung, so bewegt sich unser Geschoss über 1000m in der Schwerkraft. (Siehe Grafik)
In diesem Fall ist also alles so wie man es kennt. (Wir machen es jetzt nicht extra kompliziert mit Schuss ist auch Horizontal Parabel, Schwerkraft nimmt mit Höhe ab usw. ... können wir hier in diesem Rahmen vernachlässigen und würde das Thema sprengen)
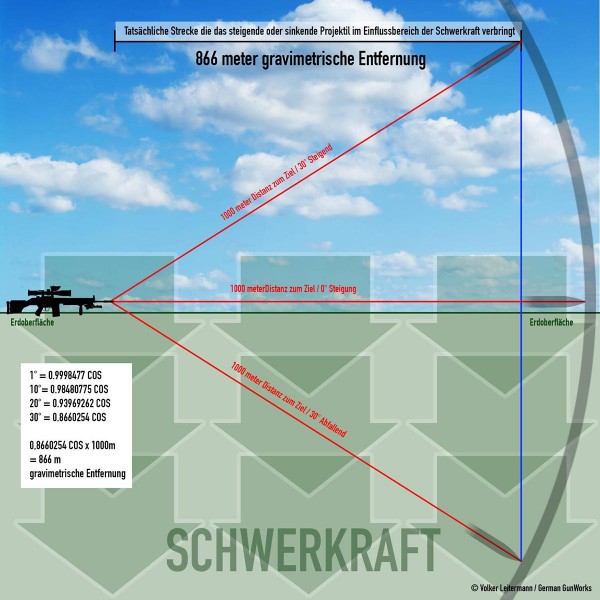
Schießen wir aber von unserem Schützenstand auf einmal den Berg hoch oder hinunter, wird die Gravimetrische Entfernung relevant. Euer Ziel ist weiterhin 1000m entfernt - jedoch verbringt das Geschoss nicht die 1000m auch im Einfluss der Schwerkraft. (Siehe Grafik) Da die Schwerkraft den Körper senkrecht nach unten zieht, ist das Geschoss also lediglich unter deren Einfluss in einer gedachten Horizontalen zum Ziel.
In unserem Beispiel liegt unser Ziel 1000m entfernt und 30° überhöht. Das Geschoss verbringt also physikalisch gerade einmal 866m unter Einflussnahme der Schwerkraft. Als Schütze muss man also um das Ziel genau zu treffen den Schuss so berechnen, als wäre das Ziel lediglich 866m entfernt - ansonsten geht der Schuss über das Ziel drüber.
Ein wichtiges Hilfsmittel ist hierbei ein ACI (Angle Cosine Indicator) - Ein Schusswinkelkompensator. Aus eigener Erfahrung greife ich gerne auf den Sniper Tools ACI Mil-Spec zurück, da dieser ein zuverlässiger Helfer in der Schussberechnung ist. Wer genug Vertrauen in die Technik hat, kann aber zwischenzeitlich auch auf eine Vielzahl an Laserentfernungsmesser zurückgreifen, da die meisten auch ein Programm zur "Schussberechnung" haben, was nichts anderes ist als das was ich hier aufzeige.
Es spielt von daher auch keine Rolle ob Ihr nach oben oder unten schießt, ein Ziel auf anderer Höhe ist gravimetrisch betrachtet immer näher als die direkte Linie zwischen Mündung und Ziel.
Grad in Kosinus
+/- 0° = 1 Kosinus
+/- 5° = 0,9961947 cos
+/- 10° = 0,98480775 cos
+/- 15° = 0,96592583 cos
+/- 20° = 0,93969262 cos
+/- 25° = 0,90630779 cos
+/- 30° = 0,8660254 cos
+/- 35° = 0,81915204 cos
+/- 40° = 0,76604444 cos
+/- 45° = 0,70710678 cos
Kosinus aus Grad ausrechnen:
Am Einfachsten nehmt Ihr einen guten Taschenrechner, gebt dort die Grad Zahl (X°) ein, die Ihr gemessen habt und drückt auf die „cos“ Taste. Er spuckt Euch dann direkt das Ergebnis in Kosinus für Eure Berechnung aus.
Keiner berechnet ernsthaft im Feld den Kosinus über die Winkelfunktion per Hand – wäre auch unnötig. Was möglich ist um auf die Gravimetrische Strecke zu kommen ist die Berechnung über den Pythagoras, denn Ihr habt ja anhand Eurer Messung bereits den Alpha Winkel und die Entfernung zum Ziel.
Kommen wir aber zum Rechenbeispiel anhand des Schaubildes mit den 30°.
Bei einem Schuss in die Höhe oder Tiefe, bei dem das Ziel 30° von meiner Schussposition weiter oben oder unten ist aber 1000m Luftlinie entfernt ist, rechne ich wie folgt:
0,866 Cos x 1000m = 866m gravimetrische Entfernung.
Ich klicke also mein ZF so, wie wenn das Ziel 866m entfernt wäre, obwohl es 1000m Luftlinie entfernt ist.
Mit dem Sniper Tools ACI wird Euch auch ohne Taschenrechner direkt der Kosinuswert angezeigt. Zeigt der ACI Euch (wenn Ihr auf dem Ziel seid) über den Strich z.B. "87" an, wisst Ihr, dass Ihr einen Kosinus von 0,87 habt. Diesen Wert müsst Ihr dann einfach noch mit der Entfernung multiplizieren und Ihr habt die gravimetrische Entfernung. Euer Kopf ist dabei der Taschenrechner, Zettel und Stift können unterstützen und da der ACI ein mechanisches Gerät ohne Batterien ist, funktioniert all das unter jedweden Umständen.
Die Formel lautet daher:
Cos-Wert x Entfernung (in m) = Gravimetrische Entfernung (in m)
Diese Grundlage solltet Ihr beherrschen. Wenn dieses Fundament vorhanden ist, dann könnt Ihr Euch auch das Leben vereinfachen, indem Ihr an Eurer Waffe einen ACI (Angle Cosine Indicator) oder zu Deutsch einen Schusswinkelkompensator (SWK) anbringt, auf welchem Ihr immer anhand der Neigung Eurer Waffe den Cosinus-Wert ablesen könnt. Moderne, gute Laserentfernugnsmesser bestimmen die Neigung im übrigen ebenfalls.
Selbstverständlich ist diese Rechnung sehr einfach gehalten und all das hier dient dem rudimentären Verständnis um was es geht. Genau genommen ist das Thema deutlich komplexer, denn je höher man schießt, desto mehr nimmt die Luftdichte, Temperatur ab – anders herum genau so. Auch muss man bedenken, dass ein Projektil in keiner geraden Linie fliegt, sondern in einer ballistischen Kurve und somit wieder etwas mehr Zeit im Schwerkrafteinfluss verbringt usw. … Der wichtigste Einfluss auf das Projektil ist aber hiermit hoffe ich verständlich erläutert.